В ЕГЭ по математике есть 4 задачи по геометрии, одна из них — задача повышенной сложности по планиметрии. Планиметрия — это геометрия на плоскости.
В ЕГЭ по математике есть 4 задачи по геометрии, одна из них — задача повышенной сложности по планиметрии. Планиметрия — это геометрия на плоскости.
Задачи по планиметрии требуют совершенно иного, нежели задачи по алгебре. Для этих задач невозможно составить некоторый набор алгоритмов, поэтому прежде всего необходим достаточный опыт их решения.
Пройдите тест с автопроверкой по геометрии, узнайте, готовы ли вы к задачам первой части Составим список того, что нужно знать для подготовки к задаче 16 по планиметрии:
Составим список того, что нужно знать для подготовки к задаче 16 по планиметрии:
1.Основные геометрические факты
a.Признаки равенства треугольников
b.Признаки подобия треугольников
c.Где располагается центр вписанной и описанной окружности в треугольнике
- особенно центр вписанной и описанной окружности в прямоугольном треугольнике
d.Факты про углы и параллельные прямые
e.Факты про углы и окружность
-
- вписанный угол
- центральный угол
- угол между касательной и хордой
- вписанный и описанный четырехугольник
f.Средняя линяя: треугольник, трапеция
2.Основные геометрические формулы
a.Формулы площадей треугольников (все!)
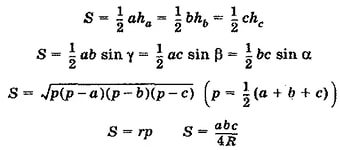
b.Формулы площади трапеции, параллелограмма
c.Теоремы синусов, косинусов, Пифагора
d.Биссектриса и отношение сторон, формула биссектрисы
e.Свойства медиан треугольника, формула медианы
f.»Степень точки» относительно окружности:
-
- Теорема о хордах
- Теорема о секущей и касательной
- Теорема о секущих
- Равенство касательных
3.Негеометрические умения
a.Уметь выражать sin a, cos a, tg a, ctg a через одно из них
b.Уметь выражать тригонометрические функции двойных и половинных углов
c.Уметь выполнять действия с дробями
d.Уметь вовремя остановиться и проверить себя, исключить ошибку по невнимательности
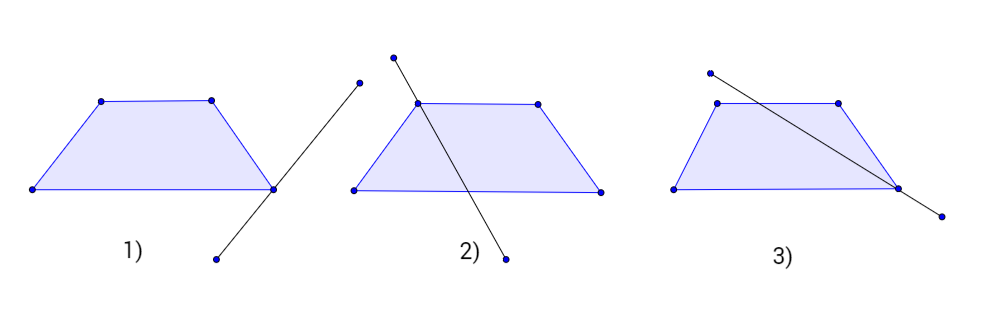
Также в задачах по планиметрии повышенной сложности следует учитывать многовариантность — различные варианты построения чертежа (может быть 2-3 варианта). Например:
-
- прямая проходит через вершину трапеции — какую вершину?
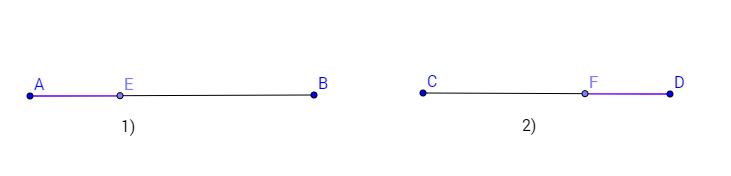
- точка делит сторону в отношении 1:3 — с какой стороны?
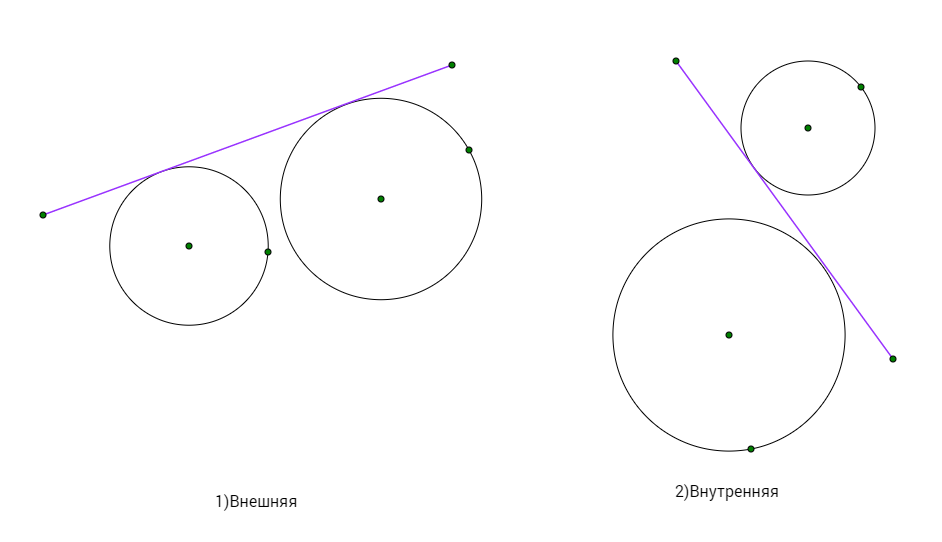
- общая касательная — внешняя или внутренняя?
Вывод: найдите сразу, где возможна многовариантность.
Оценка:
3 балла — полное решение,
2 балла — 1 вариант,
1 балл — арифметическая ошибка.
Для формул и опорных задач рекомендуется завести отдельную тетрадь «Теория» и записывать туда всю информацию. Тогда вам легко будет найти нужную формулу или теорему. Главное — постоянно тренироваться в решении задач.
Статья подготовлена по материалам видеолекции Молчанова Е.Г. «Экспресс подготовка к ЕГЭ от МФТИ, задачи С4».